Fermat’s spiral
Whoa, holy crap. I sat down to try to understand Fermat’s spiral a little bit better last night, and I ended up with a pretty cool animation.
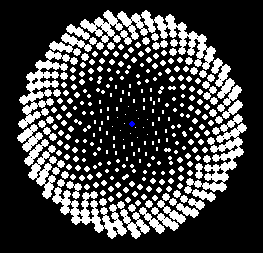
I started with the Wikipedia page, and there I saw this image, with the following caption:

The pattern of florets [say, of a sunflower], produced by Vogel’s model, (central image). The other two images show the patterns for slightly different values of the angle.
Those “other two images” had me wondering… for what different values of the angle? I wanted to see what the curve would look like with different angles (see the equations provided on that page), so I wrote a little script with my new favorite programming package, pygame, creating one big loop from 0° to 360°. Some very interesting patterns result!
(Click on image above to view video. It may take a few minutes to load, depending on your connection speed. A much smaller video is available here.)
The only thing changing here is the angle in the second equation (top left of video). c is just a constant to stretch things out whatever amount, and n is all the integers from 1 to 140 (so we get 140 dots per changing angle = 140 dots in every video frame). r is the radius of each dot from the faint gray dot in the center of the window, and Θ is the angle of each dot’s location, with 0° straight right up. At 137.5° (the golden angle), you see a tight packing of dots that is just like the arrangement of flowers/florets in a sunflower.
When do you think the pattern will repeat?
Addendum/Correction: Since I originally posted this, I rewrote the code in Processing, and discovered that I had an error that is evident in the movie in this post. I don’t know why I didn’t notice it before. You can see the error kick in around when Θ = n x 37° … More and more dots show up in the wrong position, soon after resulting in some major weirdo non-spiral action (as is clearly evident at, for example, 44.4°). This error is the result of me treating radian values as if they are values in degrees. Dammit, if this doesn’t catch me again!
Still looks neat, though. ^_^
3 Comments
- Anita replied:
500 dots, sized proportional to radius, using golden angle of 137.5°…
June 26th, 2007 at 7:14 pm. Permalink.
- Brent Fitzgerald replied:
lovely. great to see you using pygame for visual experiments like this.
June 27th, 2007 at 2:17 am. Permalink.
- karlo sostaric replied:
my new vision double spirale (spheric helix, yin yang!
authorSeptember 24th, 2007 at 3:31 am. Permalink.